Matematika Aritmetika Algebra vzorečky
Popis stránky *
• Matematika Aritmetika Algebra vzorečky
• Tahák k opakování vzorečků nejen pro studenty, ale i pro ty, kteří si chtějí oprášit vědomosti.
Posunout na obsah
• Matematika Aritmetika Algebra vzorečky
• Tahák k opakování vzorečků nejen pro studenty, ale i pro ty, kteří si chtějí oprášit vědomosti.
Posunout na obsah
Info
Matematika Aritmetika Algebra vzorečky •
• Tahák k opakování vzorečků nejen pro studenty, ale i pro ty, kteří si chtějí oprášit vědomosti.
Posunout na obsah
Matematika Aritmetika Algebra vzorečky •
• Tahák k opakování vzorečků nejen pro studenty, ale i pro ty, kteří si chtějí oprášit vědomosti.
Posunout na obsah
Koronavirus (COVID-19) - info - odkazy - mapy - statistiky
Procenta
Vytýkání
Zlomky
Přímá úměra
Mocniny
Odmocniny
Polynom - mnohočlen
Zkrácené vzorce násobení - úprava mnohočlenů (a + b)²
Logaritmy
Faktoriál
Procenta, promile, úrok
Vysvětlivky:Vytýkání
Zlomky
Přímá úměra
Mocniny
Odmocniny
Polynom - mnohočlen
Zkrácené vzorce násobení - úprava mnohočlenů (a + b)²
Logaritmy
Faktoriál
Procenta, promile, úrok
² ³ mocnina; √() druhá odmocnina toho, co je v závorce. √a druhá odmocnina a; ÷ děleno; * krát; ≥ větší, nebo rovno; ± plus, nebo mínus; ∑ = Alt+8721 (symbol součtu); R Real Numbers/ reálné číslo; N Natural numbers; // komentář
Násobení je vlastně sčítání, kde jedno číslo udává, kolikrát.
5 * 10 = 10 + 10 + 10 + 10 + 10;
Vytýkání jednoduché
Zjednodušení vzorce.. tvar součinu. Hledáme číslo, kterým můžeme podělit čísla ve vzorci. Např.
(50 + 5b) = 5 * (10 + 1b); // dělili jsme číslem 5 oba výrazy v závorce a umístili jsme jej před závorku a za něj symbol násobení.
Vytýkání neznámé
(4x² + 8x) = x * (4x + 8) = 4x * (x + 2);
Zlomky
Krácení: čitatel i jmenovatel vydělíme stejným číslem.
Násobení: násobíme čitatel prvního zlomku s čitatelem druhého zlomku a jmenovatel s jmenovatelem.
Násobení celým číslem: násobíme jen čitatele tímto číslem.
Dělení: jeden zlomek dělíme druhým, když jeden ze zlomků obrátíme a zlomky vynásobíte.
Sčítání: zlomky můžeme sčítat, pokud mají stejného jmenovatele, pak sečteme jen čitatele. Pokud nemají stejného jmenovatele, musíme použít následující proceduru.
Do čitatele výsledku násobíme čitatel prvního zlomku proti jmenovateli druhého zl. a jmenovatel prvního proti čitateli druhého a mezi násobky vložíme příslušné znaménko sčítání, či odčítání (dle prováděné operace). Do jmenovatele výsledku pak vložíme násobek jmenovatelů obou zlomků.
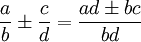
Pozor: při sčítání zlomků nemůžeme krátit napříč zlomky (jmenovatele jednoho proti čitateli druhého zlomku) jako u násobení.
Odečítání: stejně jako u sčítání, jen čitatele odečítáme.
Přímá úměra:
Cyklista ujede za hodinu průměrně 15km. Kolik ujede za 3 hodiny?
Čím více, tím více! (přímá úměra.. šipky nahoru ↑)
↑
Vytovříme zlomek po směru šipek!
15 *
x =
x = 45;
Nepřímá úměra:
Cyklista ujede za hodinu průměrně 15km a trasu ujede za 4 hodiny.
Za jak dlouho ujede stejnou trasu při rychlosti 30km/h?
Čím více, tím méně! (času,tím kratší/rychleji!) (nepřímá úměra.. první šipka dolů ↓ druhá nahoru ↑)
↓
Vytovříme zlomek po směru šipek!
4 *
x =
x = 2;
Cyklista stejnou trasu ujede za 2 hodiny.
Mocniny:
a 0 = 1; když a ≠ 0;
a³ = a * a * a;
(a * b)n = an * bn;
a m * a n = a m + n;
a m ÷ a n = a m - n; když a ≠ 0;
Odmocniny:
n√(a * b) = n√a * n√b; a,b ≥ 0;
n√(
n√(m√a) = n*m√a;
n√0 = 0;
n√1 = 1;
1√a = a;
Mnohočlen - polynom
Obecný zápis polynomu:
anxn + an-1xn-1 + ... + a1x1 + a0x0, (kde an ≠ 0 )
an se nazývají koeficienty polynomu a n je stupeň polynomu - nejvyšší exponent proměnné x s nenulovým koeficientem. (např. x³ je třetí stupeň. )
Odbornější zápis:
p(x) =
Sčítaní mnohočlenů musíme vždy vybírat členy se stejným exponentem u proměnné.
(axn) + (bxn) = (a + b)xn
Odečítání polynomů stejně jako u sčítání, pouze druhý polynom vynásobíme minus jedničkou, tj. zaměníme všechna znaménka v závorce i znaménko před závorkou a pak už klasicky sčítáme. Příklad:
(5x² + 8x) - (3x² + 7x) = (5x² + 8x) + (-3x² - 7x)
Dělení polynomů
Členy na obou stranách setřídíme dle velikosti exponentu sestupně a můžeme provést i sčítání.
(4x³ + 8x²) ÷ 2x²;
Nyní první člen prvního polynomu vydělíme prvníme členem druhého polynumu (druhý polynom obsahuje jen jeden člen).
4x³ ÷ 2x² =
Vynásobíme náš dočasný výsledek s druhým mnohočlenem, tedy s mnohočlenem, kterým dělíme.
2x * (2x²) = 4x³;
Tento výsledek odečteme od celého prvního polynomu.
Výsledek vydělíme prvním členem druhého mnohočlenu.
8x² ÷ 2x² = 4;
Tento výsledek přičteme k dočasnému (předchozímu) výsledku.
2x + 4;
Znovu vynásobíme (nyní výsledkem 4 ) celý druhý polynom.
2x² * 4 = 8x²;
Opět odečteme od dočasného výsledku.
Bylo dosaženo 0 a tím je dělení u konce.
Zkoušku provedeme zpětným násobením výsledku proti druhému mnohočelnu.
(2x + 4) * (2x²) = (4x³ + 8x²);
Zkrácené vzorce násobení - úprava mnohočlenů
(a + b)² = a² + 2ab + b²;
(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc;
(√a + √b)² = a + 2√(ab) + b = a + b + 2√(ab);
(a - b)² = a² - 2ab + b²;
(√a - √b)² = a - 2√(ab) + b = a + b - 2√(ab);
a² + b² = (a + b)² - 2ab = (a - b)² + 2ab;
a² - b² = (a-b)*(a+b);
Logaritmy
Eulerovo číslo: e = 2,718 281 828…
Logaritmická funkce:
y = logax; a ∈ R, a > 0, a ≠ 1;
Věty o logaritmech:
a>0, a≠1; x1 a x2 jsou libovolná kladná reálná čísla;
loga(x1 * x2) = loga x1 + loga x2;
loga(
loga xr = r * loga x; ∀r ∈ R Real Numbers;
loga n√x =
loga 1 = 0 (a0 = 1);
loga a = 1 (a1 = a);
aloga x = loga ax = x;
Vypočítat logaritmus o jiném základu:
loga x =
místo bé dosadit Eulerovo číslo
loga x =
Faktoriál
Faktoriál čísla n je roven součinu všech celých kladných čísel, která jsou menší nebo rovna číslu n.
Značíme vykřičníkem např. faktoriál čísla 5:
5! = 5 * 4 * 3 * 2 * 1 = 120.
Procenta
1 ‰ (promile) je jedna tisícina z celku = 0,001.
1 % (procento) je jedna setina z celku = 0,01. (Celek děleno 100)
10 % - deset procent (mezera mezi číslem a symbolem).
10% - desetiprocentní (bez mezery mezi číslem a %).
Např. 20 % z 400. Můžeme 400 ÷ 100 * procenta, nebo
20 % z 400 = 20 setin * 400 = 0,20 * 400;
Kolik procent je p z Y? p dělíme 1 %; Např. 40 kusů z celku 200? 40 děleno 1 % z 200 = 40 ÷ (200 ÷ 100) = 20 %;
Úrok výpočet
dlužná částka =
Úrok dalším rokem se zvětší, o dlužnou částku.
Když si půjčíme 100 na 10% úrok, za rok budeme již dlužit 110 a pokud jsme nesplatili, budeme platit další rok úrok již z této částky - složený úrok - dlužná částka se úročí několikrát.
Pokud nebudeme schopni splácet ani úrok, nikdy dlužnou částku nesplatíme a můžeme přijít i o dům.
5 * 10 = 10 + 10 + 10 + 10 + 10;
Vytýkání jednoduché
Zjednodušení vzorce.. tvar součinu. Hledáme číslo, kterým můžeme podělit čísla ve vzorci. Např.
(50 + 5b) = 5 * (10 + 1b); // dělili jsme číslem 5 oba výrazy v závorce a umístili jsme jej před závorku a za něj symbol násobení.
Vytýkání neznámé
(4x² + 8x) = x * (4x + 8) = 4x * (x + 2);
Zlomky
čitatel
/
jmenovatel
;Krácení: čitatel i jmenovatel vydělíme stejným číslem.
Násobení: násobíme čitatel prvního zlomku s čitatelem druhého zlomku a jmenovatel s jmenovatelem.
a
/
c
*
b
/
d
=
ab
/
cd
Násobení celým číslem: násobíme jen čitatele tímto číslem.
Dělení: jeden zlomek dělíme druhým, když jeden ze zlomků obrátíme a zlomky vynásobíte.
Sčítání: zlomky můžeme sčítat, pokud mají stejného jmenovatele, pak sečteme jen čitatele. Pokud nemají stejného jmenovatele, musíme použít následující proceduru.
Do čitatele výsledku násobíme čitatel prvního zlomku proti jmenovateli druhého zl. a jmenovatel prvního proti čitateli druhého a mezi násobky vložíme příslušné znaménko sčítání, či odčítání (dle prováděné operace). Do jmenovatele výsledku pak vložíme násobek jmenovatelů obou zlomků.
a
/
b
±
c
/
d
=
ad ± bc
/
bd
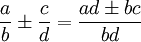
Pozor: při sčítání zlomků nemůžeme krátit napříč zlomky (jmenovatele jednoho proti čitateli druhého zlomku) jako u násobení.
Odečítání: stejně jako u sčítání, jen čitatele odečítáme.
Přímá úměra:
Cyklista ujede za hodinu průměrně 15km. Kolik ujede za 3 hodiny?
Čím více, tím více! (přímá úměra.. šipky nahoru ↑)
↑
1 hod..............15 km
3 hod......................x
↑3 hod......................x
Vytovříme zlomek po směru šipek!
3
/
1
=
x
/
15
;15 *
3
/
1
= x;x =
45
/
1
;x = 45;
Nepřímá úměra:
Cyklista ujede za hodinu průměrně 15km a trasu ujede za 4 hodiny.
Za jak dlouho ujede stejnou trasu při rychlosti 30km/h?
Čím více, tím méně! (času,tím kratší/rychleji!) (nepřímá úměra.. první šipka dolů ↓ druhá nahoru ↑)
↓
15 km/h..............4 hod
30 km/h..............x hod
↑30 km/h..............x hod
Vytovříme zlomek po směru šipek!
15
/
30
=
x
/
4
;4 *
15
/
30
= x;x =
60
/
30
;x = 2;
Cyklista stejnou trasu ujede za 2 hodiny.
Mocniny:
a 0 = 1; když a ≠ 0;
a³ = a * a * a;
(a * b)n = an * bn;
a m * a n = a m + n;
a m ÷ a n = a m - n; když a ≠ 0;
Odmocniny:
n√(a * b) = n√a * n√b; a,b ≥ 0;
n√(
a
/
b
) =
n√a
/
n√b
; a,b ≥ 0; n√(m√a) = n*m√a;
n√0 = 0;
n√1 = 1;
1√a = a;
Mnohočlen - polynom
Obecný zápis polynomu:
anxn + an-1xn-1 + ... + a1x1 + a0x0, (kde an ≠ 0 )
an se nazývají koeficienty polynomu a n je stupeň polynomu - nejvyšší exponent proměnné x s nenulovým koeficientem. (např. x³ je třetí stupeň. )
Odbornější zápis:
p(x) =
n∑i=0
aixi =
a0+
a1x +
a2x² + ... +
anxn, (kde an ≠ 0 )Sčítaní mnohočlenů musíme vždy vybírat členy se stejným exponentem u proměnné.
(axn) + (bxn) = (a + b)xn
Odečítání polynomů stejně jako u sčítání, pouze druhý polynom vynásobíme minus jedničkou, tj. zaměníme všechna znaménka v závorce i znaménko před závorkou a pak už klasicky sčítáme. Příklad:
(5x² + 8x) - (3x² + 7x) = (5x² + 8x) + (-3x² - 7x)
Dělení polynomů
Členy na obou stranách setřídíme dle velikosti exponentu sestupně a můžeme provést i sčítání.
(4x³ + 8x²) ÷ 2x²;
Nyní první člen prvního polynomu vydělíme prvníme členem druhého polynumu (druhý polynom obsahuje jen jeden člen).
4x³ ÷ 2x² =
4
/
2
x3 - 2
= 2x;Vynásobíme náš dočasný výsledek s druhým mnohočlenem, tedy s mnohočlenem, kterým dělíme.
2x * (2x²) = 4x³;
Tento výsledek odečteme od celého prvního polynomu.
(4x³ + 8x²)
-(4x³)
8x²
-(4x³)
8x²
Výsledek vydělíme prvním členem druhého mnohočlenu.
8x² ÷ 2x² = 4;
Tento výsledek přičteme k dočasnému (předchozímu) výsledku.
2x + 4;
Znovu vynásobíme (nyní výsledkem 4 ) celý druhý polynom.
2x² * 4 = 8x²;
Opět odečteme od dočasného výsledku.
(4x³ + 8x²)
-(4x³)
8x² - (8x²) 0
-(4x³)
8x² - (8x²) 0
Bylo dosaženo 0 a tím je dělení u konce.
Zkoušku provedeme zpětným násobením výsledku proti druhému mnohočelnu.
(2x + 4) * (2x²) = (4x³ + 8x²);
Zkrácené vzorce násobení - úprava mnohočlenů
(a + b)² = a² + 2ab + b²;
(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc;
(√a + √b)² = a + 2√(ab) + b = a + b + 2√(ab);
(a - b)² = a² - 2ab + b²;
(√a - √b)² = a - 2√(ab) + b = a + b - 2√(ab);
a² + b² = (a + b)² - 2ab = (a - b)² + 2ab;
a² - b² = (a-b)*(a+b);
Logaritmy
Eulerovo číslo: e = 2,718 281 828…
Logaritmická funkce:
y = logax; a ∈ R, a > 0, a ≠ 1;
Věty o logaritmech:
a>0, a≠1; x1 a x2 jsou libovolná kladná reálná čísla;
loga(x1 * x2) = loga x1 + loga x2;
loga(
x1
/
x2
) = loga x1
- loga x2;
loga xr = r * loga x; ∀r ∈ R Real Numbers;
loga n√x =
1
/
n
loga x; ∀n ∈ N;
loga 1 = 0 (a0 = 1);
loga a = 1 (a1 = a);
aloga x = loga ax = x;
Vypočítat logaritmus o jiném základu:
loga x =
logb x
/
logb a
;místo bé dosadit Eulerovo číslo
loga x =
ln x
/
ln a
;Faktoriál
Faktoriál čísla n je roven součinu všech celých kladných čísel, která jsou menší nebo rovna číslu n.
Značíme vykřičníkem např. faktoriál čísla 5:
5! = 5 * 4 * 3 * 2 * 1 = 120.
Procenta
1 ‰ (promile) je jedna tisícina z celku = 0,001.
1 % (procento) je jedna setina z celku = 0,01. (Celek děleno 100)
10 % - deset procent (mezera mezi číslem a symbolem).
10% - desetiprocentní (bez mezery mezi číslem a %).
Např. 20 % z 400. Můžeme 400 ÷ 100 * procenta, nebo
20 % z 400 = 20 setin * 400 = 0,20 * 400;
Kolik procent je p z Y? p dělíme 1 %; Např. 40 kusů z celku 200? 40 děleno 1 % z 200 = 40 ÷ (200 ÷ 100) = 20 %;
Úrok výpočet
dlužná částka =
dlužná částka * úroková míra
/
100
;
Úrok dalším rokem se zvětší, o dlužnou částku.
Když si půjčíme 100 na 10% úrok, za rok budeme již dlužit 110 a pokud jsme nesplatili, budeme platit další rok úrok již z této částky - složený úrok - dlužná částka se úročí několikrát.
Pokud nebudeme schopni splácet ani úrok, nikdy dlužnou částku nesplatíme a můžeme přijít i o dům.




